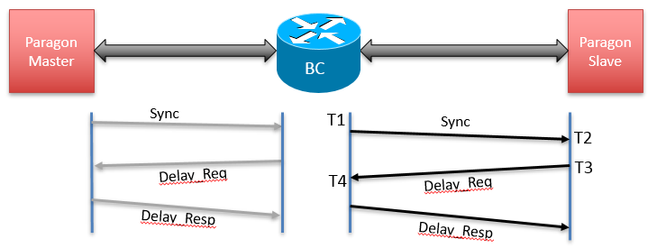
The calculations for PDV and Time Error are very similar. Both are based on packet timestamps. The diagram below shows the messages involved and the associated timestamps (using a BC as an example):
PDV
PDV is calculated in the forward direction using the timestamps carried in the Sync messages (T1) and in the reverse direction using the timestamps carried in Delay-Response messages (T4). T2 and T3 are the timestamps from the test equipment (Paragon, Sentinel). For each message transaction (i), the calculations are:
| Sync PDV | dfwd(i) = T2(i) - T1(i) |
|---|
| Delay Req PDV | drev(i) = T4(i) - T3(i) |
|---|
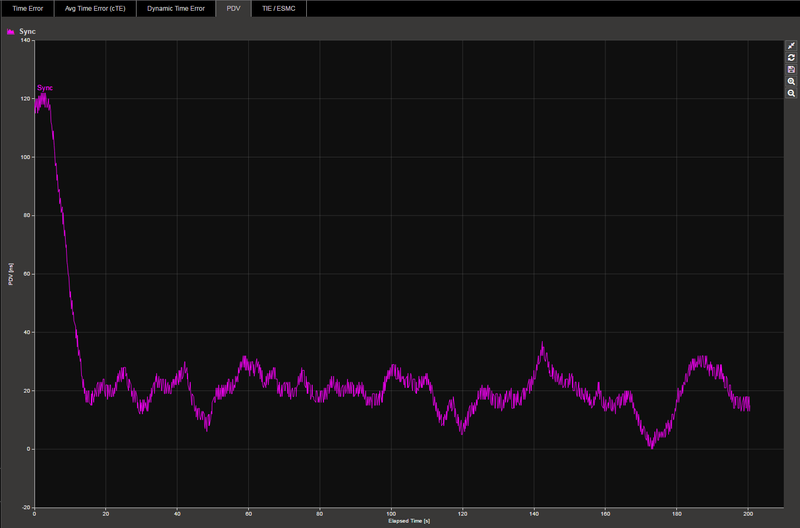
The PDV values above are then plotted against time. Since PDV is about delay variation, the PDV result is normalised to the lucky packet (the packet with the shortest delay).
Time Error
Time Error is calculated using the same timestamps as PDV. For each message transaction (i), the calculations are:
| T1 Time Error (T1TE) | TET1(i) = T1(i) - T2(i) |
|---|
| T4 Time Error (T4TE) | TET4(i) = T4(i) - T3(i) |
|---|
| 2Way Time Error (2WayTE) | TE2Way(i) = (TET1(i) + TET4(i)) / 2 |
|---|
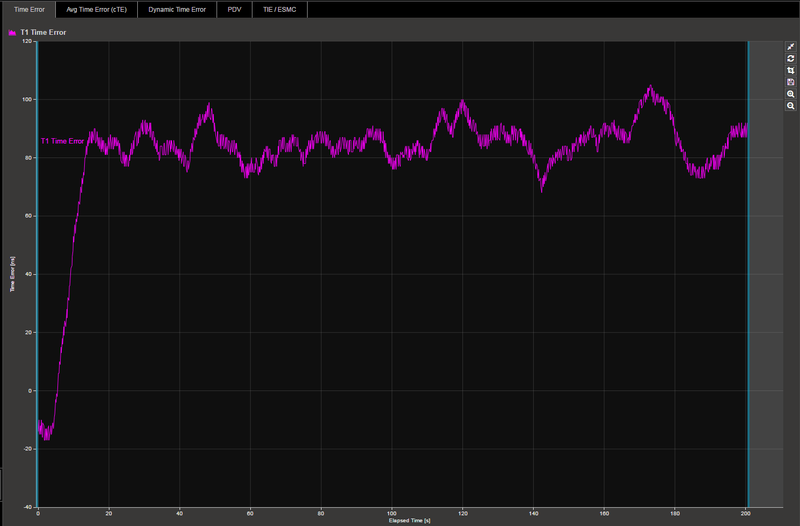
The Time Error is then plotted against time.
PDV Compared to Time Error
From the above, it follows that the Sync PDV graph will be inverted compared to the T1TE. In addition, PDV is normalised to the lucky packet and will always be positive. For example:
Sync PDV:
T1 Time Error:
The Delay-Req PDV will have the same shape as T4TE but Delay-Req is normalised to the lucky packet and will always be positive.



